| | |
|
These experiments are designed to give students a clear view of the salient properties of positive definite
The first test measures the response of the three systems to a step force (or torque) input. As seen in Figure 1, the resulting steady state position data is seen to be parabolic, linear, and constant for the respective type 2, 1, and 0 systems. The velocity and acceleration data shows the first and second derivatives with respect to time in each case. The systems are then given an impulsive input which causes linear, constant, and zero valued steady state positions respectively. For all three systems, the initial acceleration is identical (common mass properties) under the step input and the initial velocities are the same under the impulse. In addition, it is shown that the response of a given system to particular input is qualitatively similar to that of the next higher system type to the derivative of the input (e.g. step response of type 1 and impulse response of type 2).

Figure 1. Time Domain Data Shows the Distinctive Responses of Semidefinite and Positive Definite Systems The harmonic response is then obtained for each system using ECP's sine sweep function. The test data seen in Figure 2 shows the characteristic shapes with low frequency slopes of 0, -20, and -40 Db/decade** for the respective type 0, 1, and 2 systems. High frequency slope is -40 Db/decade in all cases. In the case of the lightly damped oscillator, the transient oscillation (damped) frequency is virtually identical to the harmonic oscillation frequency.
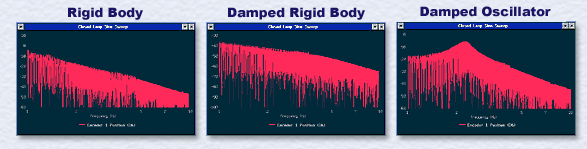 Figure 2. Sine Sweep Data Reveals the Characteristic Gain Slopes at Low and High Frequency The time domain forced responses and harmonic responses are correlated and students find that the initial time domain transient dynamics coincide with the high frequency harmonic behavior, and the steady state time domain behavior coincides with the very low frequency harmonic response. For all tests, comprehensive exercises are provided to assure that students relate the experimental results to the underlying theory.
* Here system "type" is the number of integrators or characteristic roots at the origin. | |