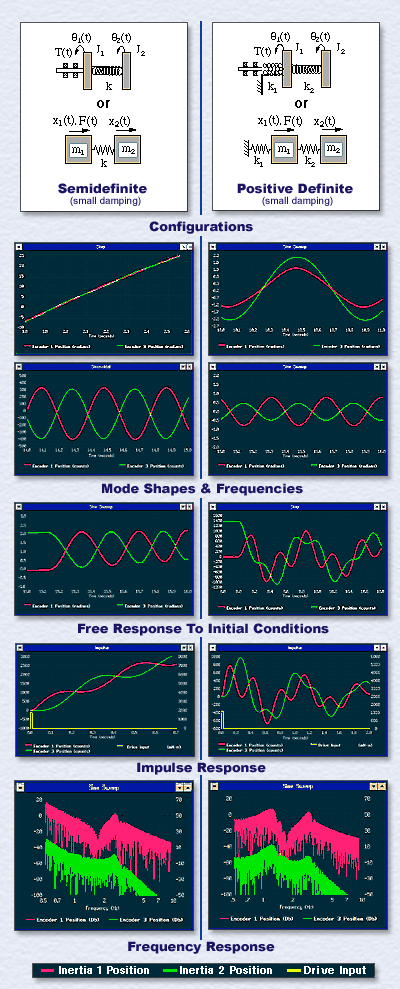
Figure 1. Experiments Demonstrate a Variety of Important Multi-DOF Principles

• Mode shapes and frequencies
• Orthogonality and linear independence of the modes
• Modal analysis and modal coordinates
• Positive definite and semidefinite behavior including the rigid body mode
• The effect of changes in inertia and stiffness
• Free and forced system responses
• Superposition of the modes in the output response
• Frequency domain phase and magnitude properties
• Poles and zeros

Figure 1 shows a small portion of the many interesting test results. The upper data gives the mode shapes and frequencies. These are found both through initializing the system in the mode shape and measuring the free response and through harmonic excitation at the modal frequency.

The third row of plots gives the free response to a static displacement where the contribution of each mode to the total output is clearly shown. The next row gives the impulse response of the two systems (or equivalently the free response to an initial velocity at the fist inertia. Again, the output is the superposition of the two modal responses.

In the bottom row, the frequency response is plotted using 's unique input trajectory and data plotting options (plots displaced by 20 Db for viewing clarity). Several key principles are demonstrated. At low frequency the semi- and positive definite systems show arbitrarily large (-40 Db/dec) and constant amplitudes respectively while at high frequency the first inertia attenuates at -40 Db/dec and the second inertia at -80 Db/dec for both systems. The first inertia has a zero (antiresonance) interspersed in frequency between the poles (resonances, pole at origin for semidefinite) and the second inertia has no zero for both systems. Phase measurements show the -180 degree shift with the poles and +180 degree with the zeros. From this, the mode shapes and frequencies are inferred directly from the amplitude data alone.

For all tests, comprehensive exercises relate the underlying principles to the behavior physically witnesed thereby building a bridge between theory and practice.